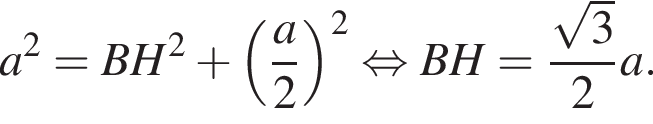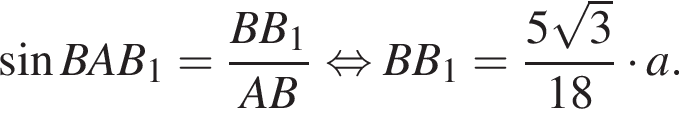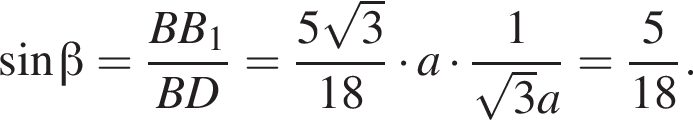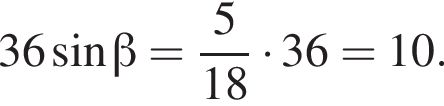Диаметр окружности пересекает хорду под углом 60° и точкой пересечения делит ее на отрезки длиной 2 и 12. Найдите квадрат радиуса окружности.
В окружности радиуса 13 проведена хорда АВ. Точка М делит хорду AВ на отрезки длиной 10 и 12. Найдите расстояние от точки М до центра окружности.
Две окружности с центрами A и B касаются в точке M. Найдите длину отрезка CN, если
 и диаметр большей окружности на 25 больше радиуса меньшей окружности.
и диаметр большей окружности на 25 больше радиуса меньшей окружности.
На рисунке изображены две окружности с центрами в точках A и B. Если MK = 48, то сумма радиусов этих двух окружностей равна:
Если MK — диаметр, O — центр окружности,
 (см. рис.), то градусная мера вписанного угла NMK равна:
(см. рис.), то градусная мера вписанного угла NMK равна:
Плоскость, удаленная от центра сферы на 8 см, пересекает ее по окружности длиной 12π см. Найдите площадь сферы.
Из точки А к окружности проведены касательные AB и АС и секущая AM, проходящая через центр окружности О. Точки В, С, M лежат на окружности (см. рис.). Найдите величину угла AOB, если

Точки A, B, C разделили окружность так, что градусные меры дуг AB, BC, CA в указанном порядке находятся в отношении 5 : 7 : 6. Найдите градусную меру угла ABC.
Из точки A к окружности проведены касательные AB и AC и секущая AM, проходящая через центр окружности O. Точки B, С, M лежат на окружности (см. рис.). Известно, что BK = 4, AC = 9. Найдите длину отрезка AK.
Четырёхугольник ABCD вписан в окружность. Если 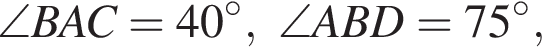 то градусная мера между прямыми AB и CD равна ...
то градусная мера между прямыми AB и CD равна ...
Длины сторон параллелограмма относятся как 4 : 5, а высота, проведенная к большей стороне, равна 6. Найдите значение выражения ![]() где S — площадь параллелограмма, если один из углов параллелограмма равен 120°.
где S — площадь параллелограмма, если один из углов параллелограмма равен 120°.
Дан параллелограмм ABCD, 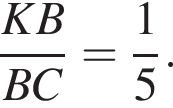 Отрезок DK пересекает сторону АВ в
Отрезок DK пересекает сторону АВ в
В равнобедренную трапецию, площадь которой равна 115, вписана окружность радиуса 5. Найдите периметр трапеции.
Четырехугольник MNPK, в котором ∠N = 128°, вписан в окружность. Найдите градусную меру угла K.
Равнобедренная трапеция с основаниями длиной 7 и 3 и острым углом 60° вращается вокруг прямой, содержащей ее боковую сторону. Найдите объем тела вращения V и в ответ запишите значение выражения ![]()
В равнобокой трапеции большее основание вдвое больше каждой из остальных сторон и лежит в плоскости α. Боковая сторона образует с плоскостью α угол, синус которого равен ![]() Найдите 36sinβ, где β — угол между диагональю трапеции и плоскостью α.
Найдите 36sinβ, где β — угол между диагональю трапеции и плоскостью α.


 а значит,
а значит, 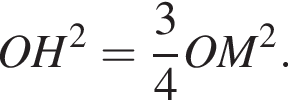 Следовательно,
Следовательно, 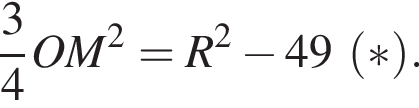
 откуда
откуда  Подставляя в (⁎), получаем:
Подставляя в (⁎), получаем: 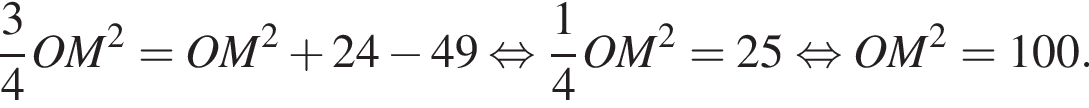
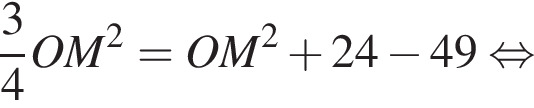
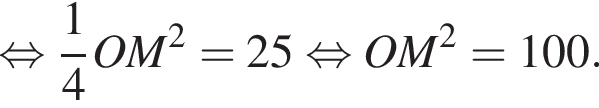
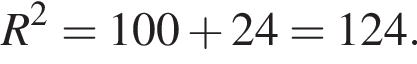
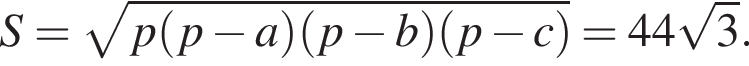
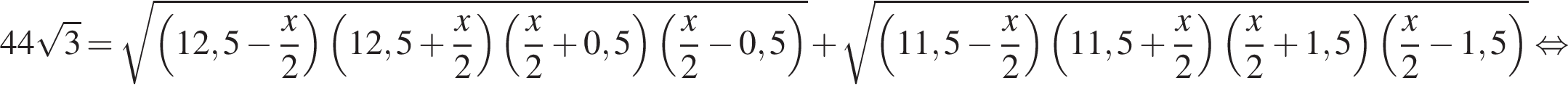

 Значит, длина отрезка
Значит, длина отрезка 
 откуда r = 6. Тогда по теореме Пифагора радиус сферы равен
откуда r = 6. Тогда по теореме Пифагора радиус сферы равен 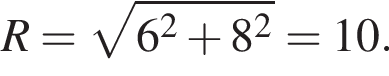 Для площади сферы имеем:
Для площади сферы имеем: 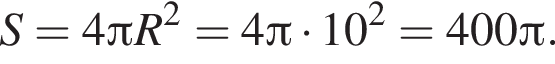
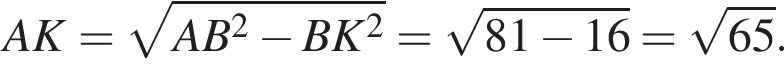


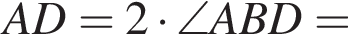

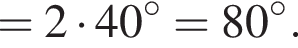
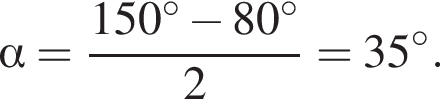
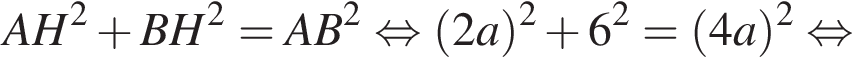
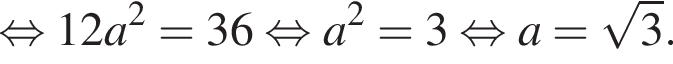
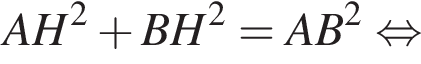
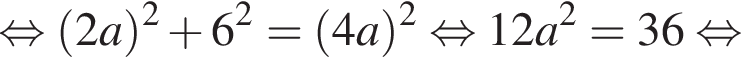

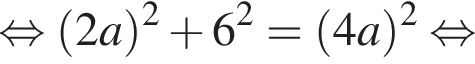
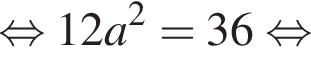
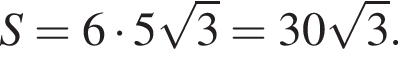 Значение выражения
Значение выражения 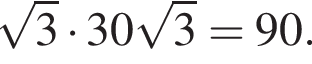
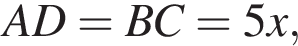 тогда
тогда  и
и 
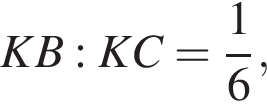 поэтому
поэтому 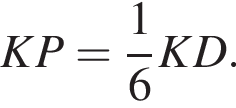
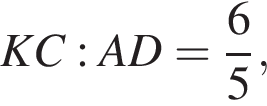 поэтому
поэтому 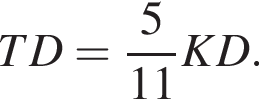
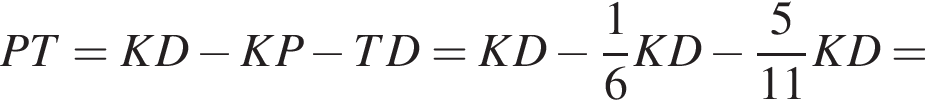
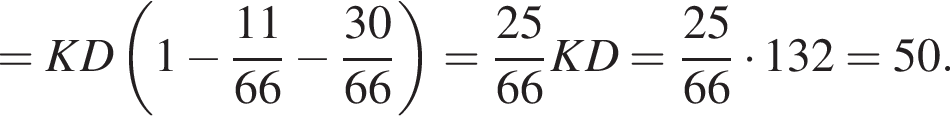
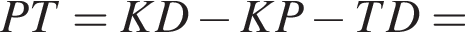
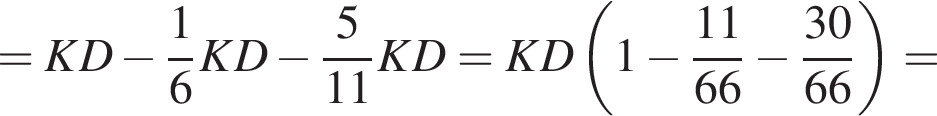
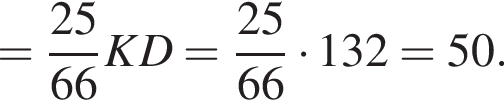
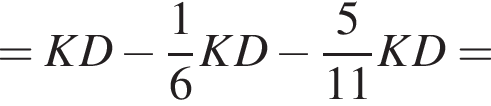
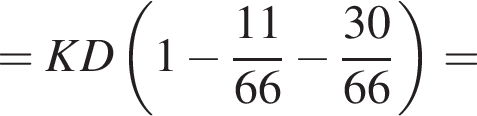
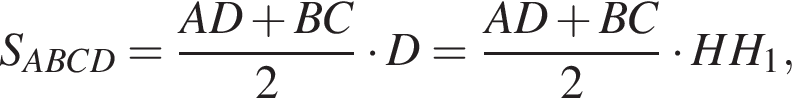 откуда получим:
откуда получим: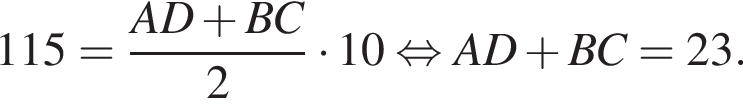
 следовательно, имеем:
следовательно, имеем:
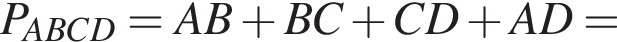
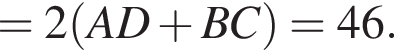



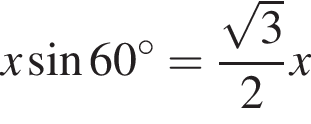 и потому объем двух таких конусов равен
и потому объем двух таких конусов равен 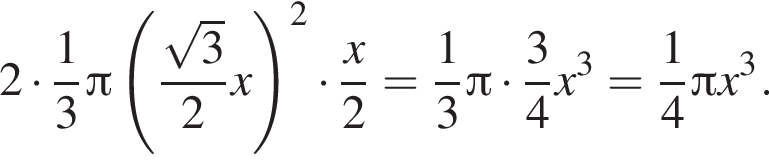
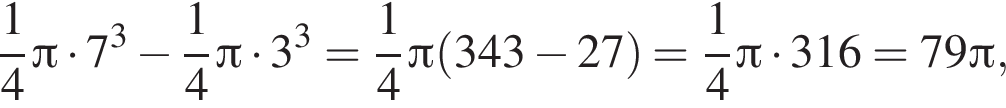
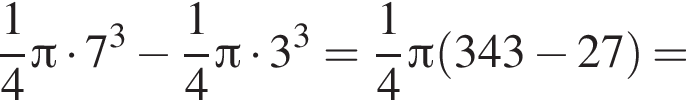
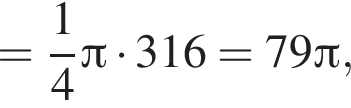
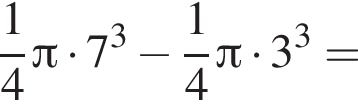
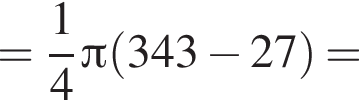
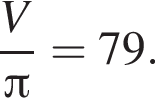
 Поскольку все стороны трапеции, кроме большего основания равны a, получим
Поскольку все стороны трапеции, кроме большего основания равны a, получим  Тогда
Тогда